Олимпиадные задачи – это особый раздел математики, к которому всегда проявляли интерес как взрослые, так и дети. Такие задачи иначе называют занимательными или нестандартными. Как правило, для их решения недостаточно школьных знаний и умений, нахождение правильного ответа требует особого подхода, творческого мышления, логического рассуждения. Олимпиадные задачи помогают приобщиться к миру науки, показать красоту и величие математики, заинтересовать в ее изучении.
Решение математических заданий такого типа способствует развитию не только математического мышления, но и творческих способностей, логики, внимательности, сообразительности, улучшает гибкость ума. Как правило, в школе мало времени уделяют этому разделу, но такие задания встречаются довольно часто в различных тестированиях, при поступлении в школы, на конкурсах и т.д. Поэтому очень важно уметь их решать и начинать с наиболее распространённых и простых вариантов ещё в детстве.
Основные принципы решения
Нет универсального способа для решения олимпиадных заданий. Существует большое количество различных типов заданий и, соответственно, много способов нахождения ответа. Но нужно всегда учитывать главные принципы при решении любых нестандартных задач:
• Внимательно прочитать текст задачи, осознать его.
• Подобрать всевозможные способы решения задачи.
• Обязательно проверить полученный результат на правдоподобность.
Несмотря на большое разнообразие олимпиадных заданий, некоторые из них схожи по структуре, способу решения или информативным данным. В соответствии с этим созданы классификации таких задач. Правда, не все из них можно отнести к определённому типу.
Типичные олимпиадные задачи для начальных классов
1. Математические ребусы
Это небольшие задания, которые, как правило, предполагают знание математических действий и наличие вычислительных навыков. Сюда же можно отнести магические квадраты, треугольники.
Примеры:
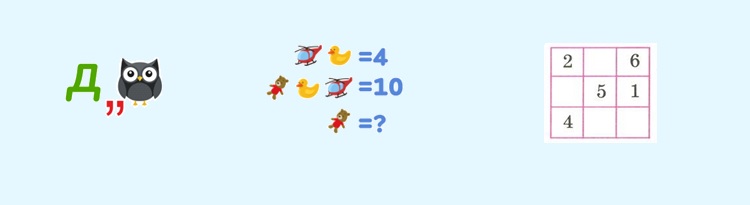
Ответы: два; 6; в магическом квадрате в первой строке – 7, во второй – 9, в третьей – 3, 8.
2. Геометрические задачи
Для решения такого типа заданий нужны знания геометрических фигур, их свойств и особенностей строения. Чаще всего это задания на подсчёт количества фигур в рамках одного треугольника, квадрата и др., построения фигур из счетных палочек.
3. Задачи на пространственное мышление
Задания, данные которых представлены в виде картинок, фигур, которые требуется мысленно переворачивать, передвигать, разрезать и т. п.
Примеры:
1. Какого элемента не хватает в кубе?
2. Развертка какого куба представлена?
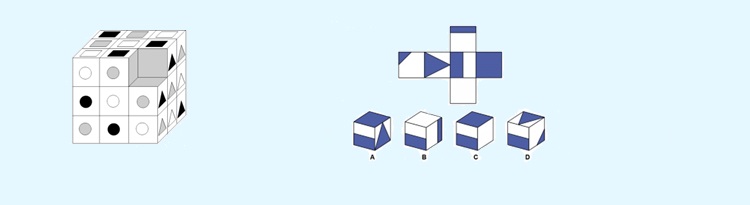
1 ответ: кубик с чёрным кругом, серым квадратом и белым треугольником
2 ответ: с
4. Задачи на внимание
Такой тип учит детей работать с информацией, изображением и текстами. Как правило, не требуют особых математических навыков. К этому типу можно отнести задания на нахождение отличий, тени от предмета, двух одинаковых предметов или текстовые задачи на внимание наподобие следующих:
Меня зовут Аня. У моего брата только одна сестра. Как зовут сестру моего брата?
Из дома в школу шли пятеро первоклассников: Петя, Лиза, Гриша, Толя, Лариса, и 3 второклассника: Семен, Стас, Ваня. Сколько девочек шли в школу?
Ответы: Аня, 2 девочки.
5. Задачи на «переливание»
Задачи не требуют особых знаний в измерении жидкости, но при этом нужно уметь последовательно рассуждать, выстраивать логические цепочки. Задачи на переливание делятся на два типа: когда можно добавлять сколько угодно воды, например из озера, и когда нужно отмерить определённое количество жидкости из уже имеющегося.
При этом решение лучше записывать в виде таблицы.
Пример:
У Насти 2 ведра объёмом 8 и 3 литра. В 8-литровом ведре налито все имеющееся у Насти молоко. Как отмерить 2 литра молока? Все излишки можно отдать Коту Пушку, который просто обожает это лакомство.
Решение:
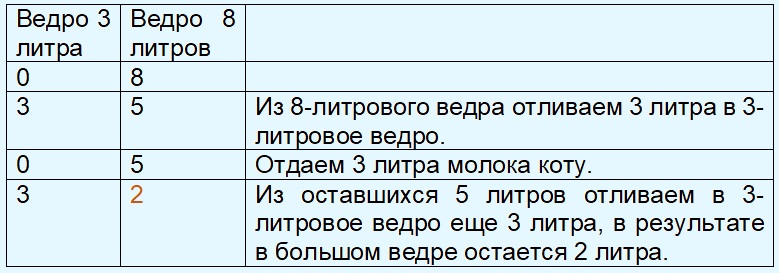
6. Задачи на взвешивание
Такой тип может потребовать знания единиц массы, а также умение логически рассуждать при поиске ответа.
Пример:
Среди трех монет одна фальшивая. Как с помощью чашечных весов без гирь найти фальшивую монету?
Решение:
Шаг 1
Возьмем 2 монеты и взвесим их на весах. Если весы уравновесятся, то оставшаяся фальшивая.
Шаг 2
Если одна тяжелее другой, то сравним ту, что тяжелее с оставшейся, если они равны, то легкая монета фальшивая.
Шаг 3
Если не равны, то сравниваем последнюю, и ту, что была легче. Монета с отличным от других весом и будет фальшивой.
7. Задачи на время
Требует знания единиц времени, умение оперировать с этими единицами, складывать вычитать и др.
Примеры:
1. 22 марта Наташа сказала: «Позавчера оставалась неделя до моего дня рождения». Когда она будет вспоминать, что неделю назад был ее день рождения?
2. Один будильник спешит на 25 минут и показывает 7 часов 50 минут. Какое время показывает другой будильник, который отстает на 15 минут?
Ответы: 3 апреля, 7 часов 10 мин.
8. Задачи на группировку, классификацию, нахождение лишнего
Упражнения, требующие широкого кругозора, умения выделять главные свойства среди прочих или находить общие свойства.
9. Комбинаторные задачи
Учат детей анализировать, составлять всевозможные комбинации, пересчитывать предметы. Для перечисления комбинаций лучше всего составлять таблицы.
Примеры:
Сколько всевозможных вариантов обедов можно составить из двух блюд (одного первого, одного второго) В меню имеется два первых блюда – щи, борщ, три вторых – рыба, гуляш, плов.
Ответ: 6 вариантов
В коробке 6 белых и 4 красных шара. Из коробки наугад достают шары. Какое максимальное количество шаров нужно вытащить, чтобы точно достать 1 белый?
Ответ: предположим, что нам не везёт, тогда всегда будут попадаться красные шары. Их всего 4, значит на 5 раз точно будет белый.
10. Логические задачи
Один из самых широких типов заданий, так как нужно обладать большим спектром математических знаний, уметь рассуждать, анализировать. Сюда относятся различные задания по типу решения и рассуждения.
Примеры:
У бабушки есть гуси и кролики. У них вместе 25 голов и 58 лапок. Сколько гусей и сколько кроликов у бабушки?
Решение: предполагаем, что все гуси. Тогда лап у них будет 25*2=50, осталось 8. У кроликов больше лап, чем у гусей на 2, значит 8:2=4 кролика и 21 гусь. Проверка: 4*4= 16 лап, 21*2= 42 лапы, 16+42=58 лап.
По вертикальному столбу высотой 6 м движется улитка. За день она поднимается на 4 м, за ночь опускается на 3 м. Сколько дней ей потребуется, чтобы добраться до вершины?
Решение: За первые сутки улитка поднялась на высоту 1 м. В конце вторых суток она будет на высоте 2 м: 1 + 4- 3 = 2. В конце третьего дня улитка достигнет вершины: 2 + 4 = 6 (м).
На улице гуляли три подруги в разных платьях (в красном, синем и жёлтом). Какого цвета платье у Кати, если Маша не в синем платье, а Оля не в жёлтом и не в синем.
Решение (легче всего решать с помощью таблицы):
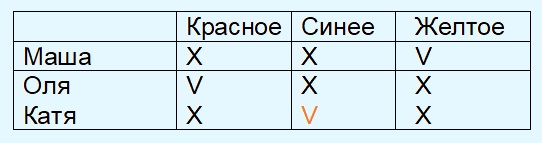
Решать олимпиадные задания всегда очень увлекательно и интересно, особенно в кругу семьи. Это отличный способ с пользой провести время с близкими, а также подготовить своего ребёнка к математическим турнирам. Чем чаще тренироваться, тем выше будет результат такой работы.
