Изучение основ геометрии является важной частью учебного плана начальной школы. Одной из основных и сложных тем становится изучение периметра, площади и объема. У детей 1-4 класса только начинает развиваться абстрактное мышление, именно по этой причине такие задания даются им с трудом. Поэтому при изучении этих тем рекомендуется использовать наглядные материалы, такие как геометрические фигуры, модели и конструкторы. Это поможет малышам лучше понять абстрактные понятия.
Способы знакомства с понятиями периметр, площадь и объем
В 1 классе обучение предполагает знакомство с базовыми понятиями геометрии, на основе чего строится дальнейшая программа. Периметр и площадь фигур обычно изучают во 2 классе.
Изучение периметра
Дети начинают изучение этой темы во втором классе. Обычно, когда они уже знакомы с основами геометрии, умеют складывать числа в пределах 100 и знают простые способы умножения, учитель вводит понятие периметра. Затем проводятся практические упражнения на нахождение периметра простых геометрических фигур, таких как квадраты и прямоугольники. Далее рассматриваются более сложные: треугольники, многоугольники и составные фигуры.
Способы знакомства:
1. Возьмите проволоку, согните из неё прямоугольник. Пусть ребенок назовет фигуру и объяснит ее особенности. Для того чтобы узнать периметр, нужно сложить длины всех сторон: разогните проволоку, покажите, что все стороны составляют вместе один отрезок, длина которого и будет являться периметром. Также можно напомнить, что прямоугольник — это замкнутая линия, а чтобы найти её длину, достаточно сложить длины всех ее звеньев.
2. Нарисуйте прямоугольник и раскрасьте его равные стороны цветными карандашами. Теперь начертите отрезки в соответствии со сторонами прямоугольника. На чертеже будет хорошо видно, что весь отрезок состоит из частей, равных всем сторонам фигуры. Поэтому, чтобы узнать периметр, необходимо сложить длины всех сторон: а+b+a+b. Так как противоположные стороны равны, то можно сократить запись: (a+b)×2. Это и будет периметр. Аналогично разберите периметр квадрата.
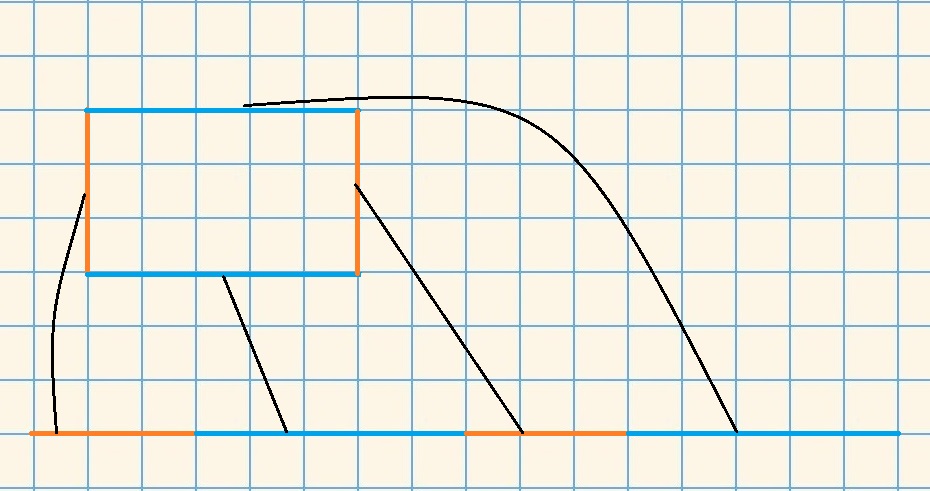
Что ребенок должен запомнить:
- Периметр — это сумма длин всех сторон фигуры, то есть длина границы или контура этой фигуры.
- Периметр обозначается буквой P.
- Формула периметра прямоугольника: P=(a+b)×2
- Формула периметра квадрата P=4a
Изучение площади
Обычно изучение площади начинается после того, как дети усвоят понятие периметра. Учитель объясняет, как рассчитывать площадь квадрата и прямоугольника, используя формулы. Также проводятся практические упражнения, включающие нахождение площади комбинированных фигур.
Способы знакомства:
1. Первоначально нужно дать понять малышу, что площадь — это внутренняя часть фигуры или плоскость. Для этого можно взять тетрадь обвести её на листе бумаги или газеты. Затем вырезать получившуюся фигуру. Это и будет площадь.
2. Начертите с ребенком на клетчатой бумаге два различных прямоугольника и вырежьте их. Малыш уже знает, что внутренняя часть — это площадь фигуры. Попросите сравнить, какая площадь больше. Например, наложите прямоугольники друг на друга. Если один полностью поместился на другом, то можно сказать, что его площадь меньше, но если ровно наложить не получается, нужно вычислить их площади и сравнить числовые значения. Предложите посчитать клетки внутри каждого прямоугольника. Покажите ребенку, что каждый раз пересчитывать их долго и не всегда возможно, нужно придумать более быстрый способ. Посчитайте в первом прямоугольнике количество клеток в строке (а=5) и количество таких строк (b=3), если 5×3=15, получаем аналогичный ответ, как при пересчитывании клеток. Значит, чтобы найти площадь, нужно длину прямоугольника умножить на ширину.
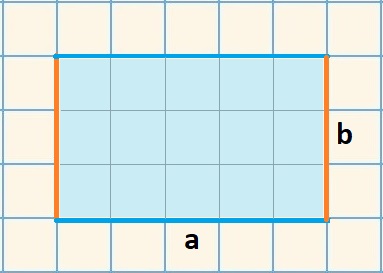
Теперь найдите площадь у второго прямоугольника, сравните с предыдущими результатами. Аналогично вычислите площадь квадрата.
3. Используйте конструктор Лего. Подготовьте квадратные детали конструктора. Соберите из них прямоугольник, ставя детали рядом. Как описано выше в пункте 2, можно сначала посчитать количество всех используемых для строительства деталей, это будет площадь фигуры. Затем можно посчитать количество кубиков в строке и в столбце. Умножение этих чисел дает такой же результат, но быстрее. Потренируйтесь составлять различные прямоугольники и находить их площадь. Затем предложите составить фигуру, площадь которой равна 24 или 18. В этом случае вариантов может быть несколько.
Что ребенок должен запомнить:
- Площадь — это плоскость, то есть внутренняя часть фигуры, ограниченная контуром.
- Площадь обозначается буквой S.
- Формула площади прямоугольника S=a×b
- Формула площади квадрата S=а×а
Площадь и периметр
Сразу после изучения площади или даже одновременно стоит давать задания на повторение периметра для избежания путаницы в этих понятиях. При этом важно соблюдать некоторые правила и применять особые методы:
- Учите находить площадь и периметр у одной и той же фигуры.
- Разделите по цветам записи, касающиеся периметра и площади. Например, когда записывается формула периметра и его вычисление, путь ребенок делает это только зелёной ручкой, а когда площади — чёрной. Такое разграничение помогает не путать эти два понятия между собой через зрительное восприятие и очень облегчает понимание на начальном этапе.
- Применяйте игровые задачи по типу: дядя Ваня решил завести козу и построил для нее загон. Нужно посчитать, какая будет длина забора и сам луг для выпаса козы. При этом нужно сделать рисунок и обозначить одним цветом забор, а другим — место для выпаса.
- Покажите практическую значимость данных понятий. Например, предложите ребенку представить, что нужно поклеить обои на стену и рассчитать сколько потребуется полос обоев или определить длину светодиодной ленты для украшения потолка по периметру комнаты.
- Игра с кубиком на листочке — хороший способ закрепить знания о площади и периметре. Нужно: 2 кубика, лист в клетку и цветные карандаши для каждого участника. Первый игрок кидает два кубика, выпавшие числа обозначают стороны прямоугольника. Нужно сначала вычислить периметр прямоугольника. Например: выпали числа 5 и 6, тогда Р=(5+6)*2=22 клетки. Его нужно начертить на листке бумаги. Потом ребенок должен начертить другие возможные прямоугольники с таким же периметром — длину сторон можно менять, но периметр должен оставаться неизменным: в нашем случае стороны могут быть 4 и 7, 3 и 8. В середине каждой фигуры необходимо записать площадь. Обратите внимание ребенка, что у прямоугольников с одинаковым периметром может быть разная площадь. Когда лист закончится, подсчитывается общая площадь "захваченной" территории и определяется победитель.
Изучение объема
Объем — это измерение трехмерного пространства. В начальной школе дается понятие объема для жидкости, например, литр молока, трехлитровая банка компота и др.
Вычисление объёма изучается в средних классах. Учитель объясняет детям, что объем рассчитывается путем умножения площади основания на высоту фигуры. Также проводятся практические упражнения, включающие расчет объема комбинированных фигур.
Способы знакомства:
1. Для начальной школы: знакомство происходит на основе практической работы, а именно переливание жидкости из одной емкости в другую. Обозначение единицы измерения — литр.
2. Для средней школы: самый наглядный метод использовать кубики или конструктор Лего. Построить из деталей параллелепипед. Затем предложить ребенку рассмотреть его. В основе фигуры лежит прямоугольник. Как вычислить его площадь, ребенок уже знает (a×b). Теперь нужно посчитать сколько рядов в высоту составляет вся фигура (с). Значит, чтобы узнать объем фигуры, нужно умножить все три значения: длину, ширину и высоту (a×b×c).
Важно!
- Для измерения объема требуется три параметра: ширина, высота и длина, поэтому ответ записывается в кубических единицах, то есть см³, дм³, м³.
- Для измерения площади нужно два параметра: ширина и длина, поэтому в ответе квадратные единицы измерения: см², дм², м².
- Для измерения периметра достаточно знать только один параметр, а именно длину, поэтому в ответе единицы измерения записываются так: мм, см, дм, м.
Изучение периметра, площади и объема является важной частью учебной программы. Понимание этих понятий позволяет детям развивать аналитические способности и логическое мышление. Используя правильные подходы и методы, родители и учителя могут помочь детям успешно освоить материал и применять его в реальной жизни.







